Factor de Seguridad vs Probabilidad de Falla

En el sector de la ingeniería siempre se debe hacer el mejor balance posible entre seguridad y economía, en ese orden.  Estas dos variables están siempre inevitablemente conectadas, a mayor seguridad menor economía y viceversa, lo que lleva a la pregunta obligada: ¿Cuándo algo es suficientemente seguro?

Muchos de nosotros fuimos educados en el concepto del Factor de Seguridad (FS), que es aquel número que nos debe indicar cuándo un diseño es suficientemente seguro, aunque es más apropiado decir que debería serlo.

Típicamente se nos ha enseñado que siempre que FS > 1 estaremos entrando en terreno seguro, sin advertirnos que de hecho no siempre es así, y que en ciertos casos un adecuado nivel de seguridad no se puede garantizar, aun para FS mucho mayores que 1. ¿Cómo es esto posible?

A pesar de la simpleza del concepto y de su evidente utilidad para aplicaciones prácticas, el uso indiscriminado del concepto de factor de seguridad puede resultar ambiguo o brindar un falso sentido de protección, sobre todo si se desconoce el carácter aleatorio de las variables involucradas.

Existe un concepto poderoso que está presente en nuestras vidas y se llama incertidumbre, que es la variabilidad inherente a la que hace referencia en el párrafo anterior.  La incertidumbre está tanto en los precios del petróleo, como en la predicción de lluvias, en la vida útil de un celular, en las utilidades de una compañía o en la estabilidad de un edificio, entre muchos otros fenómenos.  No es posible predecir con total certeza ninguna de las variables referidas, ni muchas otras variables y fenómenos de la vida real, casi todo está signado por el efecto de la incertidumbre.

En el contexto de la ingeniería tradicionalmente el factor de seguridad FS ha sido definido como la relación entre la resistencia y la fuerza o acción sobre un elemento.  Este factor debe ser siempre mayor que la unidad para garantizar una razonable protección ante las fuerzas actuantes y el valor que se especifica depende, entre otras, del tipo de material, de la carga, de la frecuencia anual de excedencia de las cargas de naturaleza estocástica y de incertidumbres asociadas a la estimación de todos los parámetros involucrados.  Así por ejemplo, para un análisis de estabilidad estático de un muro de contención se requiere que el FS sea mayor o igual a 1.5, para un análisis dinámico se requiere que sea mayor o igual a 1.1, y para estimar la capacidad portante de un suelo el FS normalmente aceptado es del orden de 3.0.  De hecho, si se tuviera absoluta certeza de que tanto la resistencia como las fuerzas tuvieran exactamente los valores calculados, el factor de seguridad podría ser ligeramente superior a 1.0,

Una metodología general que se puede utilizar para determinar la probabilidad de falla (por ejemplo falla en la operación anual desde el punto de vista de los resultados económicos, pero se puede extender a muchos otros ámbitos) se basa en la premisa fundamental de la Teoría de Confiabilidad que define la función de estado límite U, de acuerdo con la ecuación 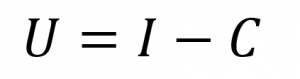(1).

(1)

Donde la utilidad U es la llamada función de estado límite, definida como la diferencia entre los ingresos I y los Costos C.  La ecuación (1) también podría escribirse en términos de resistencia y cargas, por ejemplo.

A partir de esta definición se infiere que si U < 0 el estado de desempeño es definido como inseguro, es decir que hay pérdidas; si U > 0 se tiene una condición denominada como segura (hay utilidad), y cuando U = 0 se tiene el llamado estado límite como se muestra en la Figura 1.

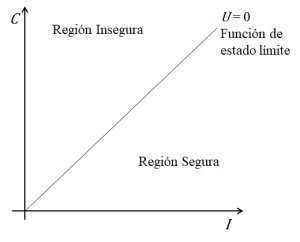Figura 1.  Función de estado límite

En la Figura 2 se muestran dos negocios que tienen los mismos ingresos y costos medios, y por tanto tienen la misma utilidad bruta promedio, que representa el factor de seguridad de la operación.  Los negocios serían iguales (el factor de seguridad es el mismo) sino fuera por la incertidumbre de cada uno de ellos, representada por la amplitud de las campanas de Gauss de las funciones de densidad de probabilidad (para el ejemplo y por facilidad gráfica se ha supuesto la misma incertidumbre en los ingresos y en los costos, pero esto por supuesto no es así en la realidad).  La zona sombreada representa el dominio en el cual los costos son superiores a los ingresos y por lo tanto representa la probabilidad de falla de cada negocio.  A mayor incertidumbre o dispersión en las funciones de densidad de probabilidad, mayor será la probabilidad de falla, dada una misma utilidad esperada.

 

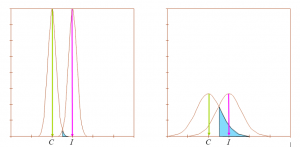Figura 2.  Comparación de negocios con igual utilidad media esperada pero con diferentes probabilidades de falla

Una manera aproximada de estimar esta probabilidad de falla es mediante el índice de confiabilidad de Hasofer – Lind, el cual se calcula por medio de la ecuación 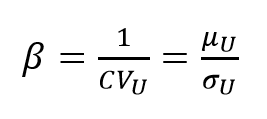(2):

(2)

Donde es el coeficiente de variación de , es la media y  es la desviación estándar de .

La media y la desviación estándar de se calculan mediante la teoría de propagación de la incertidumbre, haciendo uso de las propiedades de la esperanza como operador lineal, de manera que la media y la desviación estándar de  se calculan con las ecuaciones (3) y (4). En la ecuación (4) está implícito que los ingresos y los costos son variables aleatorias independientes, lo cual no necesariamente es cierto pero en aras de la simplicidad se mantendrá esa suposición.

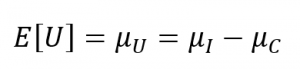(3)

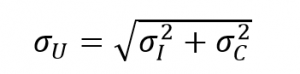(4)

Los costos  son la suma de los costos directos de los proyectos , de los costos indirectos de la empresa  y de los gastos administrativos , de acuerdo con la ecuación (5), de manera que la media y la esperanza de quedan expresados con las ecuaciones (6) y (7).

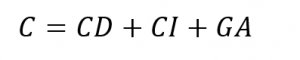(5)

(6)

(7)

Una vez obtenidos los dos primeros momentos de se procede a calcular la probabilidad de ocurrencia de un evento inseguro mediante la ecuación (8), donde es la función de probabilidad acumulada para una distribución normal estándar:

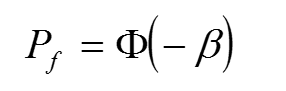(8)

De la Figura 2 se puede inferir que la sola definición de concepto de seguridad a partir del FS puede resultar incompleta y que el uso del concepto de Probabilidad de Falla P_f aporta mayor información, dada la incertidumbre asociada.

Aún para factores de seguridad altos se pueden obtener probabilidades de falla altas en algunos casos, lo que demuestra que el uso del concepto de FS no brinda información suficiente sobre el grado de seguridad real de un fenómeno físico o económico, por ejemplo.

En todo caso, no todas las variables involucradas para el cálculo de P_f deben considerarse como aleatorias, porque varias de ellas tienen influencia muy baja o despreciable en la variabilidad de los resultados.